Find x, y, z if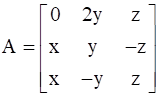 
satisfies A’ = A–1
Given,
We need to find x, y and z such that A’ = A-1
If A’ = A-1
Pre-multiplying A on both sides:
AA’ = AA-1
⇒ AA’ = I where I is the identity matrix.
∴ 
⇒ 
By matrix multiplication we have:
⇒ 
On equating the corresponding elements of matrix.
We need basically 3 equations as we have 3 variables to solve for. You can pick any three elements and equate them.
We have:
4y2 + z2 = 1 …(1)
x2 + y2 + z2 = 1 …(2)
2y2 – z2 = 0 …(3)
Adding equation 2 and 3:
6y2 = 1
⇒ y2 = 1/6
∴ 
From equation 3:
Z2 = 2y2
⇒ z2 = 2(1/6)
∴ z2 = 1/3
∴ 
From equation 2:
x2 = 1 – y2 – z2
⇒ x2 = 1 – (1/6) – (1/3)
⇒ x2 = 1 – 1/2 = 1/2
∴ 
Thus,
; 
and 
50