Express the matrix 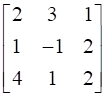as the sum of a symmetric and a skew symmetric matrix.

Question

Philoid · Accepted Answer

If A is any matrix then it can be written as the sum of a symmetric and skew symmetric matrix.

Symmetric matrix is given by 1/2(A + A’)

Skew symmetric is given by 1/2(A – A’)

And A = 1/2(A + A’) + 1/2(A – A’)

Here, A =

Symmetric matrix is given by -

⇒ 1/2(A + A’) =

Skew Symmetric matrix is given by -

⇒ 1/2(A - A’) =

∴ A =