Find which of the functions is continuous or discontinuous at the indicated points:

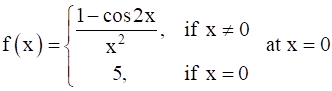
Given,

…(1)

We need to check its continuity at x = 0

A function f(x) is said to be continuous at x = c if,

Left hand limit (LHL at x = c) = Right hand limit(RHL at x = c) = f(c).

Mathematically we can represent it as-

Where h is a very small number very close to 0 (h→0)

Now according to above theory-

f(x) is continuous at x = 0 if -

Clearly,

LHL = {using equation 1}

As we know cos(-θ) = cos θ

⇒ LHL =

∵ 1 – cos 2x = 2sin²x

∴ LHL =

As this limit can be evaluated directly by putting value of h because it is taking indeterminate form (0/0)

As we know,

∴ LHL = 2 × 1² = 2 …(2)

Similarly, we proceed for RHL-

RHL =

⇒ RHL =

⇒ RHL =

Again, using sandwich theorem, we get -

RHL = 2 × 1² = 2 …(3)

And,

f (0) = 5 …(4)

Clearly from equation 2, 3 and 4 we can say that

∴ f(x) is discontinuous at x = 0