Find the value of k so that the function f is continuous at the indicated point: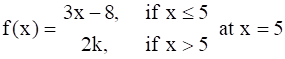

Question

Philoid · Accepted Answer

Given,

…(1)

We need to find the value of k such that f(x) is continuous at x = 5.

A function f(x) is said to be continuous at x = c if,

Left hand limit(LHL at x = c) = Right hand limit(RHL at x = c) = f(c).

Mathematically we can represent it as-

Where h is a very small number very close to 0 (h→0)

Now, let’s assume that f(x) is continuous at x = 5.

∴

As we have to find k so pick out a combination so that we get k in our equation.

In this question we take LHL = f(5)

∴

⇒ {using equation 1}

⇒ 3(5 – 0) – 8 = 2k

⇒ 15 – 8 = 2k

⇒ 2k = 7

∴ k = 7/2