Examine the differentiability of f, where f is defined by

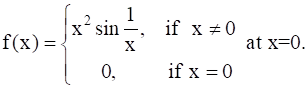
Given,

…(1)

We need to check whether f(x) is continuous and differentiable at x = 0

A function f(x) is said to be continuous at x = c if,

Left hand limit(LHL at x = c) = Right hand limit(RHL at x = c) = f(c).

Mathematically we can represent it as-

Where h is a very small number very close to 0 (h→0)

And a function is said to be differentiable at x = c if it is continuous there and

Left hand derivative(LHD at x = c) = Right hand derivative(RHD at x = c) = f(c).

Mathematically we can represent it as-

Finally, we can state that for a function to be differentiable at x = c

Checking for the continuity:

Now according to above theory-

f(x) is continuous at x = 0 if -

∴ LHL =

⇒ LHL = {using equation 1}

As sin (-1/h) is going to be some finite value from -1 to 1 as h→0

∴ LHL = 0² × (finite value) = 0

∴ LHL = 0 …(2)

Similarly,

RHL =

⇒ RHL = {using equation 1}

As sin (1/h) is going to be some finite value from -1 to 1 as h→0

∴ RHL = (0)²(finite value) = 0 …(3)

And, f(0) = 0 {using equation 1} …(4)

From equation 2,3 and 4 we observe that:

∴ f(x) is continuous at x = 0. So we will proceed now to check the differentiability.

Checking for the differentiability:

Now according to above theory-

f(x) is differentiable at x = 0 if -

∴ LHD =

⇒ LHD = {using equation 1}

⇒ LHD =

As sin (1/h) is going to be some finite value from -1 to 1 as h→0

∴ LHD = 0×(some finite value) = 0

∴ LHD = 0 …(5)

Now,

RHD =

⇒ RHD = {using equation 1}

⇒ RHD =

As sin (1/h) is going to be some finite value from -1 to 1 as h→0

∴ RHD = 0×(some finite value) = 0

∴ RHD = 0 …(6)

Clearly from equation 5 and 6,we can conclude that-

(LHD at x=0) = (RHD at x = 0)

∴ f(x) is differentiable at x = 0