Verify the Rolle’s theorem for each of the functions
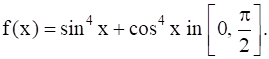
Given: f(x) = sin4x + cos4x
Now, we have to show that f(x) verify the Rolle’s Theorem
First of all, Conditions of Rolle’s theorem are:
a) f(x) is continuous at (a,b)
b) f(x) is derivable at (a,b)
c) f(a) = f(b)
If all three conditions are satisfied then there exist some ‘c’ in (a,b) such that f’(c) = 0
Condition 1:
f(x) = sin4x + cos4x
Since, f(x) is a trigonometric function and trigonometric function is continuous everywhere
⇒ f(x) = sin4x + cos4x is continuous at ![]()
Hence, condition 1 is satisfied.
Condition 2:
f(x) = sin4x + cos4x
On differentiating above with respect to x, we get
f’(x) = 4 × sin3 (x) × cos x + 4 × cos3 x × (- sin x)
![]()
⇒ f’(x) = 4sin3 x cos x – 4 cos3 x sinx
⇒ f’(x) = 4sin x cos x [sin2x – cos2 x]
⇒ f’(x) = 2 sin2x [sin2x – cos2 x]
[∵ 2 sin x cos x = sin 2x]
⇒ f’(x) = 2 sin 2x [- cos 2x]
[∵ cos2 x – sin2 x = cos 2x]
⇒ f’(x) = - 2 sin 2x cos 2x
⇒ f(x) is differentiable at ![]()
Hence, condition 2 is satisfied.
Condition 3:
f(x) = sin4x + cos4x
f(0) = sin4(0) + cos4(0) = 1
![]()
![]()
Hence, condition 3 is also satisfied.
Now, let us show that c ∈ (![]() ) such that f’(c) = 0
) such that f’(c) = 0
f(x) = sin4x + cos4x
⇒ f’(x) = - 2 sin 2x cos 2x
Put x = c in above equation, we get
⇒ f’(c) = - 2 sin 2c cos 2c
∵, all the three conditions of Rolle’s theorem are satisfied
f’(c) = 0
⇒ - 2 sin 2c cos 2c = 0
⇒ sin 2c cos 2c = 0
⇒ sin 2c = 0
⇒ 2c = 0
⇒ c = 0
Now, cos 2c = 0
![]()
![]()
![]()
![]()
Thus, Rolle’s theorem is verified.