For the function 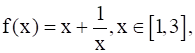 the value of c for mean value theorem is
the value of c for mean value theorem is
Mean Value Theorem states that, Let f : [a, b] → R be a continuous function on [a, b] and differentiable on (a, b). Then there exists some c in (a, b) such that
![]()
We have, ![]()
Since, f(x) is a polynomial function it is continuous on [1,3] and differentiable on (1,3).
Now, as per Mean value Theorem, there exists at least one c ∈ (1,3), such that ![]()
⇒ ![]()
⇒ ![]()
⇒ ![]()
⇒ 3(c2 – 1) = 2c2
⇒ 3c2 – 2c2 = 3
⇒ c2 = 3
⇒ ![]()
⇒ ![]()
96