Let X be a discrete random variable whose probability distribution is defined as follows:

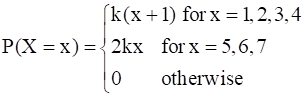
where k is a constant. Calculate

(i) the value of k (ii) E (X) (iii) Standard deviation of X.

Given:

Thus, we have the probability distribution of X is

(i) the value of k

We know that,

Sum of the probabilities = 1

∴ 2k + 3k + 4k + 5k + 10k + 12k + 14k = 1

⇒ 50k = 1

⇒ k = 0.02

(ii) To find: E(X)

The probability distribution of X is:

Therefore,

μ = E(X)

∴ E(X) = 2k + 6k + 12k + 20k + 50k + 72k + 98k + 0

= 260k

= 5.2 …(i)

(iii) To find: Standard deviation of X

We know that,

Var(X) = E(X²) – [E(X)]²

= ΣX²P(X) – [Σ{XP(X)}]²

= [2k + 12k + 36k + 80k + 250k + 432k + 686k +0] – [5.2]² = 1498k – 27.04

= 29.96 – 27.04

= 2.92

We know that,

standard deviation of X = √Var(X) = √2.92 = 1.7088

≅ 1.7