The probability distribution of a random variable x is given as under:

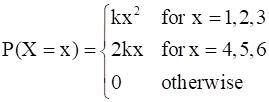
where k is a constant. Calculate

(i) E(X) (ii) E (3X²) (iii) P(X ≥ 4)

Given:

We know that,

Sum of the probabilities = 1

⇒ k + 4k + 9k + 8k + 10k + 12k = 1

⇒ 44k = 1

(i) To find: E(X)

We know that, μ = E(X)

or

E(X) = ΣXP(X)

= 1 × k + 2 × 4k + 3 × 9k + 4 × 8k + 5 × 10k + 6 × 12k

= k + 8k + 27k + 32k + 50k + 72k

= 190k

= 4.32

(ii) To find: E(3X²)

Firstly, we find E(X²)

We know that,

E(X²) = ΣX²P(X)

= 1² × k + 2² × 4k + 3² × 9k + 4² × 8k + 5² × 10k + 6² × 12k

= k + 16k + 81k + 128k + 250k + 432k

= 908k

= 20.636

≅ 20.64

∴ E(3X²) = 3 × 20.64 = 61.92

(iii) P(X ≥ 4) = P(X = 4) + P(X = 5) + P(X = 6)

= 8k + 10k + 12k

= 30k