In Figure 3, a right triangle ABC circumscribes a circle of radius r. If AB and BC are of length 8 cm and 6 cm respectively, find the value of r. (CBSE 2012)
Given,
A right-angled triangle ABC,
AB = 8 cm
BC = 6 cm
Let’s suppose Triangle ABC is right angled such that;
∠B = 90°
O be the center and
r be the radius of the incircle.
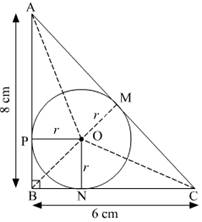
AB is a tangent to the circle at point P
BC is a tangent to the circle at point N and
CA is a tangent to the circle at point M
∴ OP = ON = OM = r (radius of the circle)
Area of ∆ABC = 1/2 ×BC×AB = 24 cm2
By Pythagoras theorem;
CA2 = AB2 + BC2
CA2 = (8)2 + (6)2
CA2 = 100 cm
CA = 10 cm
Area of ∆ABC = Area of ∆OAB + Area of ∆OBC + Area of ∆OCA
![]()
![]()
![]()
![]()
r = 2 cm
12