A circle touches the sides of a quadrilateral. Show that the angles subtended at the centre by a pair of opposite sides are supplementary. (CBSE 2012,2014)

The diagram is as follows:

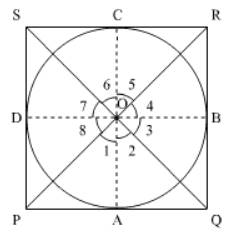
Let PQRS be the quadrilateral which has a circle inside it with center O.

Now join AO, BO, CO, DO

From the figure, ∠ 1 = ∠ 8 [Two tangents drawn from an external point to a circle subtend equal angles at the centre.]

We can also state that ∠ 2 = ∠ 3, ∠ 4 = ∠ 5 and ∠ 6 = ∠ 7

Sum of angles in a quadrilateral is 360°

Sum of angles at the center is 360°

∠ 1 + ∠ 2 + ∠ 3 + ∠ 4 + ∠ 5 + ∠ 6 + ∠ 7 + ∠ 8 = 360°

2(1 + 2 + 5 + 6) = 360°

1 + 2 + 5 + 6 = 180°

or

2(8 + 3 + 4 + 7) = 360°

8 + 3 + 4 + 7 = 180°

∠ POQ + ∠ ROS= 180°

Also ∠ QOR + ∠ POS = 180°

[Since ∠ POQ = ∠ 1 + ∠ 2

∠ ROS = ∠ 5 + ∠ 6

∠ QOR = ∠ 7 + ∠ 8

∠ POS = ∠ 3 + ∠ 4

as shown in the figure]

Hence it is proved that PQ and RS subtend supplementary angles at center.

Thus the angles subtended at the centre by a pair of opposite sides are supplementary.