In fig. 7, are shown two arcs PAQ and PBQ. Arc PAQ is a part of circle with center O and radius OP while arc PBQ is a semi-circle drawn on PQ as diameter with center M. If OP = PQ = 10 cm, show that area of shaded region is.

(CBSE 2016)

We know that,

Tangent drawn from an external point of a circle are equal

∴ OP = OQ = 10 cm

PQ = 5 + 5

= 10 cm

_{As OP = OQ = PQ}

_{∴ OP = OQ = OP = 10 cm}

_{Hence, POQ is an equilateral triangle as all the sides are equal to each other}

_{Also, angles of an equilateral triangle are of 60}^o

_{∴∠ POQ = 60}^o

_{Here, we have}

_{Side = 10 cm}

_{Radius, r = 5 cm}

⇒ θ = 60°

And, R = 10 cm

∴ Area of shaded region = Area of triangle OPQ + Area of semi-circle PBQM – Area of sector OPAQ

.

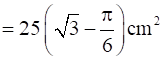Hence, proved