In a game, a man wins ₹ 5 for getting a number greater than 4 and loses ₹ 1 otherwise, when a fair die is thrown. The man decided to throw a die thrice but to quit as and when he gets a number greater than 4. Find the expected value of the amount he wins/loses.
OR
A bag contains 4 balls. Two balls are drawn at random (without replacement) and are found to be white. What is the probability that all balls in the bag are white?
Given: a man wins Rs. 5 for getting a number greater than 4 and loses Rs. 1 otherwise
To find: the expected value of the amount he wins/loses if he throws dice thrice
Let S be the success of getting number greater than 4 and F be the failure of getting number less than or equal to 4
As he quit as and when he gets a number greater than 4 i.e. S
Then sample space will be {S, FS, FFS, FFF}
Case 1: E1: gets success i.e. number greater than 4 on 1st throw
![]()
{∵ Favorable outcomes = {5, 6} = 2 &
Total outcomes = {1, 2, 3, 4, 5, 6} = 6}
He wins Rs 5
Case 2: E2: gets failure i.e. number less than or equal to 4 on 1st throw and gets success i.e. number greater than 4 on 2nd throw
![]()
He wins Rs 5 and loses Rs. 1
⇒ Amount = 5 – 1 = Rs. 4
Case 3: E3: gets failure 1st throw, gets failure on 2nd throw and gets success on 3rd throw
![]()
He wins Rs 5 and loses Rs. 2
⇒ Amount = 5 – 2 = Rs. 3
Case 4: E4: gets failure 1st throw, gets failure on 2nd throw and gets failure on 3rd throw
![]()
He loses Rs. 3
⇒ Amount = Rs. -3
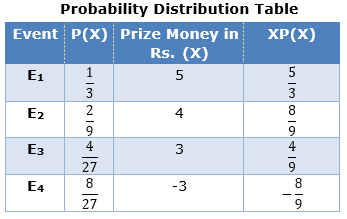
![]()
![]()
Hence, expected value of prize he wins/loses, E(X),
![]()
OR
Given: A bag contains 4 balls
To find: probability that all balls in the bag are white
Formula used:
Bayes’ Theorem:
Given E1, E2, E3....En are mutually exclusive and exhaustive events, we can find the conditional probability P(Ei|A) for any event A associated with Ei as follows:
![]()
Two balls are drawn at random (without replacement) and are found to be white. This means at least two balls are white
Now,
Let A: Two drawn balls are white
E1: All the four balls are white
E2: Three balls are white
E3: Two balls are white
Since E1, E2, E3 are mutually exclusive and exhaustive events
![]()
![]()
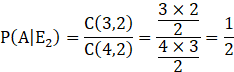
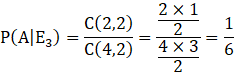
Probability that all the balls are white is given by, P(E1|A)
![]()
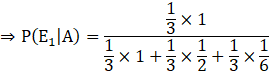
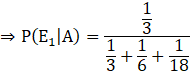
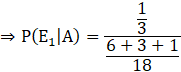
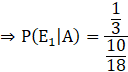
![]()
![]()
Hence, probability that all balls in the bag are white is 0.6