Differentiate with respect to x.

OR

If prove that

To find: derivative

Now,

y = u + v

Taking log both sides:

⇒ log u = log (x^{sin x})

⇒ log u = sin x log x

{∵ log (a^b) = b log a}

Differentiating both sides:

Taking log both sides:

⇒ log v = log (sin x)^{cos x}

⇒ log v = cos x log sin x

{∵ log (a^b) = b log a}

Differentiating both sides:

As,

OR

Given: 2 cos (log x) + 3 sin (log x)

Let y = 2 cos (log x) + 3 sin (log x)

Again, differentiating both sides:

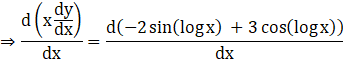
{∵ y = 2 cos (log x) + 3 sin (log x)}

Hence Proved