Find the equation of a curve passing through (2, 1) if the slope of the tangent to the curve at any point (x, y) is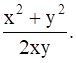

Slope of tangent is given as

Slope of tangent of a curve y = f(x) is given by

Put y = vx

Differentiate vx using product rule,

Integrate

Put 1 – v² = t hence differentiating with respect to v we get which means 2vdv = -dt

Resubstitute t

Resubstitute v

Now it is given that the curve is passing through (2, 1)

Hence (2, 1) will satisfy the curve equation (a)

Putting values x = 2 and y = 1 in (a)

Using log a + log b = loga b

Put c in equation (a)

Using log a – log b = log

Using log a + log b = log ab

⇒ 3x = 2(x² – y²)

⇒ 3x = 2x² – 2y²

⇒ 2y² = 2x² – 3x

Hence equation of curve is