Find the angle between the lines whose direction cosines are given by the equations l + m + n = 0, l2 + m2 – n2 = 0.
We are given two equations that represents the direction cosines of two lines,
l + m + n = 0 …(i)
l2 + m2 – n2 = 0 …(ii)
We need to find the angle between the lines whose direction cosines are given by the given equations.
Let us find the value of l, m and n.
From equation (i),
l + m + n = 0
⇒ n = -l – m
⇒ n = -(l + m) …(iii)
Substituting the value of n from (i) in (ii),
l2 + m2 – n2 = 0
⇒ l2 + m2 – (-(l + m))2 = 0
⇒ l2 + m2 – (l + m)2 = 0
⇒ l2 + m2 – (l2 + m2 + 2lm) = 0
⇒ l2 + m2 – l2 – m2 – 2lm = 0
⇒ l2 – l2 + m2 – m2 – 2lm = 0
⇒ -2lm = 0
⇒ lm = 0
⇒ l = 0 or m = 0
First, put l = 0 in equation (i),
Equation (i) ⇒ 0 + m + n = 0
⇒ m + n = 0
⇒ m = -n
If m = λ, then
n = -m
⇒ n = -λ
∴, direction ratios (l, m, n) = (0, λ, -λ)
![]()
![]()
Now, put m = 0 in equation (i),
Equation (i) ⇒ l + 0 + n = 0
⇒ l + n = 0
⇒ l = -n
If n = λ, then
l = -n
⇒ l = -λ
∴, direction ratios (l, m, n) = (-λ, 0, λ)
![]()
![]()
By theorem, that says
Angles between two lines whose direction ratio are d1 and d2 is θ given by,
![]()
Substituting values of d1 and d2 in θ, we get
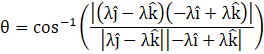
Solving numerator,
![]()
![]()
Solving denominator,
![]()
![]()
![]()
![]()
Substituting the values in θ, we get
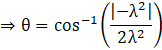
![]()
![]()
[∵, ![]() ]
]
Thus, the required angle between the given lines is π/3.