Find the distance of a point (2,4,–1) from the line

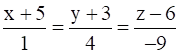
It is given that,

The point is P(2, 4, -1).

The equation of the line is .

We need to find the distance of the point P from the given line.

Always note that,

To find distance between a point and a line, get foot of perpendicular from the point on the line.

We have let,

P(2, 4, -1) be the given point and,

be the given line.

Direction Ratio of the line L is (1, 4, -9). …(i)

Let us find any point on this line.

Take the line L:

Take

⇒ x + 5 = λ

⇒ x = λ – 5

Take

⇒ y + 3 = 4λ

⇒ y = 4λ – 3

Take

⇒ z – 6 = -9λ

⇒ z = 6 – 9λ

∴, any point on the line L is (λ – 5, 4λ – 3, 6 – 9λ).

Let this point be Q(λ – 5, 4λ – 3, 6 – 9λ), the foot of the perpendicular from the point P(2, 4, -1) on the line L.

We know the direction ratio of any line segment PQ, where P(x₁, y₁, z₁) and Q(x₂, y₂, z₂), is given by (x₂ – x₁, y₂ – y₁, z₂ – z₁).

So, the direction ratio of PQ is given by

Direction ratio of PQ = (λ – 5 – 2, 4λ – 3 – 4, 6 – 9λ – (-1))

⇒ Direction ratio of PQ = (λ – 7, 4λ – 7, 6 + 1 – 9λ)

⇒ Direction ratio of PQ = (λ – 7, 4λ – 7, 7 – 9λ) …(ii)

Also, we know that

If two lines are perpendicular, then the dot products of their direction ratio is 0.

Here, PQ is perpendicular to the line L. From (i) and (ii),

Direction ratio of L = (1, 4, -9)

Direction ratio of PQ = (λ – 7, 4λ – 7, 7 – 9λ)

So,

(1, 4, -9).(λ – 7, 4λ – 7, 7 – 9λ) = 0

⇒ 1(λ – 7) + 4(4λ – 7) + (-9)(7 – 9λ) = 0

⇒ λ – 7 + 16λ – 28 – 63 + 81λ = 0

⇒ λ + 16λ + 81λ – 7 – 28 – 63 = 0

⇒ 98λ – 98 = 0

⇒ 98λ = 98

⇒ λ = 1

So, the coordinate of Q, which is the foot of the perpendicular from the point on the given line, is

Q(λ – 5, 4λ – 3, 6 – 9λ) = Q(1 – 5, 4(1) – 3, 6 – 9(1))

⇒ Q(λ – 5, 4λ – 3, 6 – 9λ) = Q(1 – 5, 4 – 3, 6 – 9)

⇒ Q(λ – 5, 4λ – 3, 6 – 9λ) = Q(-4, 1, -3)

Now, let us find the perpendicular distance from point P to the line, that is, point Q.

⇒ We need to find .

We know that,

Put λ = 1,

To find ,

Thus, distance from the given point to the given line is 7 units.