Discuss the continuity and differentiability of f(x) = |x| + |x - 1| in the interval ( - 1,2).

Question

Philoid · Accepted Answer

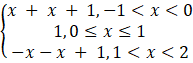
f(x) =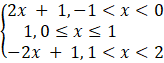

We know that a polynomial and a constant function is continuous and differentiable every where. So, f(x) is continuous and differentiable for x ( - 1,0) and x (0,1) and (1,2).

We need to check continuity and differentiability at x = 0 and x = 1.

Continuity at x = 0

= 1

F(0) = 1

Since, f(x) is continuous at x = 0

Continuity at x = 1

= 1

F(1) = 1

= 1

Since, f(x) is continuous at x = 1

For differentiability,

LHD(at x = 0) = RHD (at x = 0)

Differentiability at x = 0

(LHD at x = 0) =

=

= 2

(RHD at x = 0) =

=

= 0

Since,(LHD at x = 0)(RHD at x = 0)

So, f(x) is differentiable at x = 0.

For differentiability,

LHD(at x = 1) = RHD (at x = 1)

Differentiability at x = 1

(LHD at x = 1) =

=

= 0

(RHD at x = 1) =

=

Since, f(x) is not differentiable at x = 1.

So, f(x) is continuous on ( - 1,2) but not differentiable at x = 0, 1