Show that the function
F(x) = 
Is continuous but not differentiable at x = 1.
F(x) = 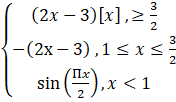
For continuity at x = 1
F(1) = - (2(1) - 3) = 1
LHL = ![]()
= ![]()
= ![]()
= sin ![]()
= 1
RHL = ![]()
= ![]()
= ![]()
= - 1( - 1)
= 1
LHL = RHL = f(1)
So, f(x) is continuous at x = 1
For differentiability at x = 1
(LHD at x = 1) = ![]()
= ![]()
= ![]()
= ![]()
= 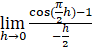
= 0
(RHD at x = 1) = ![]()
= ![]()
= ![]()
= ![]()
= ![]()
= - 2
(LHD at x = 1)![]() (RHD at x = 1)
(RHD at x = 1)
Hence, f(x) is continuous but not differentiable at x = 1.
9