The vertices of the triangle are A(5, 4, 6), B(1, -1, 3) and C(4, 3, 2). The internal bisector of angle A meets BC at D. Find the coordinates of D and the length AD.

Question

Philoid · Accepted Answer

Given: The vertices of the triangle are A(5, 4, 6), B(1, -1, 3) and C(4, 3, 2)

To find: the coordinates of D and the length AD

Formula used:

Distance Formula:

The distance between any two points (a, b, c) and (m, n, o) is given by,

Section Formula:

A line AB is divided by C in m:n where A(x, y, z) and B(a, b, c).

The coordinates of C is given by,

We know angle bisector divides opposite side in the ratio of the other two sides.

As AD is angle bisector of A and meets BC at D

⇒ BD : DC = AB : BC

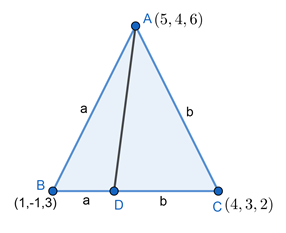
Distance between A(5, 4, 6) and B(1, -1, 3) is AB,

The distance between A(5, 4, 6) and C(4, 3, 2) is AC,

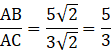
AB : AC = 5:3

⇒ BD: DC = 5:3

Therefore, m = 5 and n = 3

B(1, -1, 3) and C(4, 3, 2)

Coordinates of D using section formula:

The distance between A(5, 4, 6) and is AD,

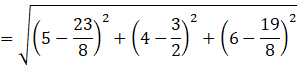
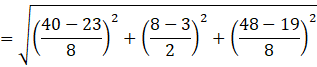
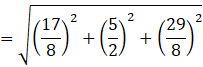
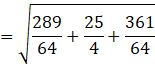
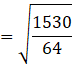
units

Hence, Coordinates of D are and the length of AD is units