The ratio in which the line joining the points (a, b, c) and (-1, -c, -b) is divided by the xy-plane is

Given: points A(a, b, c) and B(-1, -c, -b)

To find: the ratio in which the line joining given points is divided by the xy-plane

Formula used:

Section Formula:

A line AB is divided by C in m:n where A(x, y, z) and B(a, b, c).

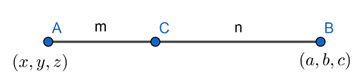
The coordinates of C is given by,

z coordinate is always 0 on xy-plane

Let Point C(x, y, 0), and C divides AB in ratio k: 1

Therefore, m = k and n = 1

A(a, b, c) and B(-1, -c, -b)

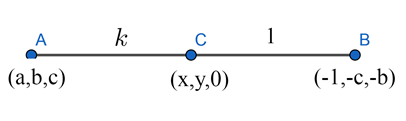
Coordinates of C using section formula:

On comparing:

⇒ -bk + c = 0(k + 1)

⇒ -bk = -c

Hence, C divides AB internally in ratio c: b