Find the equation of the hyperbola whose

focus is (a, 0), directrix is 2x + 3y = 1 and eccentricity = 2

Given: Equation of directrix of a hyperbola is 2x – y + a = 0. Focus of hyperbola is (a, 0) and eccentricity (e) =

To find: equation of hyperbola

Let M be the point on directrix and P(x, y) be any point of hyperbola

Formula used:

where e is eccentricity, PM is perpendicular from any point P on hyperbola to the directrix

Therefore,

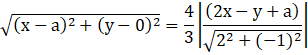
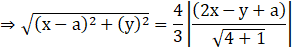
Squaring both sides:

{∵ (a – b)² = a² + b² + 2ab &

(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac}

⇒ 117{x² + a² – 2ax + y²} = 16{4x² + y² + a² – 4xy – 2ay + 4ax}

⇒ 117x² + 117a² – 234ax + 117y² = 64x² + 16y² + 16a² – 64xy – 32ay + 64ax

⇒ 117x² + 117a² – 234ax + 117y² – 64x² – 16y² – 16a² + 64xy + 32ay – 64ax = 0

⇒ 53x² + 101y² – 298ax + 32ay + 64xy + 111a² = 0

This is the required equation of hyperbola.