If e1 and e2 are respectively the eccentricities of the ellipse x^2/18 + y^2/4 = 1 and the hyperbola x^2/9 - y^2/4 = 1, then the relation between e1 and e2 is


Given: e1 and e2 are respectively the eccentricities of the ellipse and the hyperbola


To find: value of 2e12 + e22




Eccentricity(e) of hyperbola is given by,



Here a = 3 and b = 2





Therefore,



For ellipse:




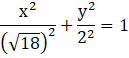
Eccentricity(e) of ellipse is given by,







Therefore,





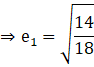
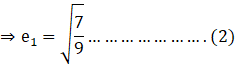
Substituting values from (1) and (2) in 2e12 + e22


2e12 + e22







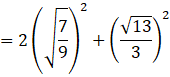
= 3


Hence, value of 2e12 + e22 is 3

2
1