For any ΔABC, show that - b (c cos A – a cos C) = c² – a²

Note: In any ΔABC we define ‘a’ as length of side opposite to ∠A , ‘b’ as length of side opposite to ∠B and ‘c’ as length of side opposite to ∠C .

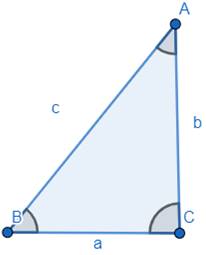
Key point to solve the problem:

Idea of cosine formula in ΔABC

• Cos A =

• Cos B =

• Cos C =

As we have to prove:

b (c cos A – a cos C) = c² – a²

As LHS contain bc cos A and ab cos C which can be obtained from cosine formulae.

∴ From cosine formula we have:

Cos A =

⇒ bc cos A = …..eqn 1

And Cos C =

⇒ ab cos C = ……eqn 2

Subtracting eqn 2 from eqn 1:

bc cos A - ab cos C = -

⇒ bc cos A - ab cos C = c² - a²

∴ b(c cos A - a cos C) = c² - a² …proved